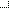انحراف معیار داده های خود را محاسبه نمایید.
|

ریشه دوم واریانس که انحراف معیار نامیده میشود دارای واحدی یکسان با متغیر اولیه است. نحوه محاسبه آن به شرح ذیل است:

واریانس و انحراف معیار بهترین شاخص ها جهت بررسی پراکندگی داده های کمی هستند.
لازم به یادآوری است در جایی که تعداد داده های ما 30 و یا کمتر از 30 باشند در مخرج کسر باید به جای N از N-1 استفاده کنیم و فرمول واریانس و انحراف معیار ما به صورت زیر خواهند بود:

و در این حالت به جای استفاده از s2 از S2 (برآورد واریانس) استفاده می کنیم. پس واریانس و انحراف معیار برای 3 عدد 300 و 200 و 100 برابر خواهد بود با:

نکته: اگر تمامی داده ها را با مقدار ثابتی جمع و یا از مقدار ثابتی کم کنیم میانگین داده های جدید به همان مقدار افزایش و یا کاهش می یابند ولی انحراف معیار و واریانس تغییر نمی کند.
به عنوان مثال اگر میانگین نمرات شرکت کنندگان در آزمون دستیاری امسال 400 و انحراف معیار نمرات آنها 10 و واریانس آن 100 باشد و سپس به تمام شرکت کنندگان 10 نمره اضافه نمایند میانگین نمرات جدید 410 خواهد بود اما انحراف معیار و واریانس همان مقادیر قبلی را خواهند داشت.
نکته: اگر تمامی داده ها را در مقدار ثابتی ضرب و یا بر مقدار ثابتی تقسیم نمائیم میانگین و انحراف معیار داده های جدید به همان مقدار بزرگ و یا کوچک می شود اما واریانس با مجذور عدد ثابت تغییر می کند. به عنوان مثال اگر متوسط طول قد دانش آموزان یک کلاس 70/1 متر و انحراف معیار قد آنها از متر باشد و بخواهیم واحد اندازه گیری طول را 1/0 متر به سانتی متر تغییر دهیم میانگین داده های جدید 170 (100 ´ 70/1)، انحراف معیار آنها 10 (100 ´ 1/0) و واریانس آنها 100 (100=000/10 ´ 01/0=1002 ´ واریانس قبلی) خواهد بود.